Our Work
We are interested in the fundamental performance bounds of
delay tolerant networks,
which is a last resort networking paradigm when direct (multi-hop) communication is not possible.
In this case, the message delivery is achieved by the store-carry-forward principle.
- Typically mobility plays crucial role in DTNs.
- DTN communication is also possible over stationary nodes as long as new nodes
join the network (before the present ones depart).
- Fundamental question is, e.g., what is the required
node density that guarantees a succesful message delivery (with
a reasonable probability).
- Message dissemination can be analyzed by studying an appropriate
continuum percolation model in space-time.
- Due to the causality, the percolation model is directed
along the time-axis.
Figure on the right illustrates the dissemination of a message in R2-plane
by epidemic routing.
- Model:
Nodes arrive to the plane according to a Poisson point process, remain stationary for a fixed time,
and then depart.
- Time-axis points to "right"
- Each cylinder corresponds to a node, and the cross-section of the cylinder and the (x,y)-plane
at time t defines the transmission range of the given node:
Overlapping cylinders means that those two nodes
are within each others' transmission range at the given time t.
- Red color indicates the source, the green color that a node has the message,
and yellow that it does not have it yet.
Nodes never acquiring the message have been omitted.
- Note that two cylinders at the start become only partially green (why?).
Each message dissemination corresponds to such a cluster in space-time.
If the node density is sufficiently high,
above the so-called critical threshold (specific to mobility pattern etc.),
then there is a positive probability P that the cluster is infinite and
the message gets
spread across the plane eventually reaching also the final destination(s).
An infinite cluster means that the system percolates.
The node density can be expressed in many ways. One intuitive quantity is the mean number
of neighbours, ν. Direct
multi-hop communication over long distances (under certain simplified assumptions)
requires that ν > 4.51, where the constant 4.51 is the critical threshold for
disks in plane, νc = 4.51.
However, if delays are tolerated, the communication in DTN fashion becomes feasible
already when ν > 1.52, which is the critical (directed) percolation threshold of
aligned cylinders [1]. Mobility decreases this bound even further (see [1] for more details).
Neglecting the causality leads to the undirected model, and the critical threshold for
aligned cylinders is νc ≈ 1.32. [2], which serves as a (quite reasonable)
lower bound.
|
|
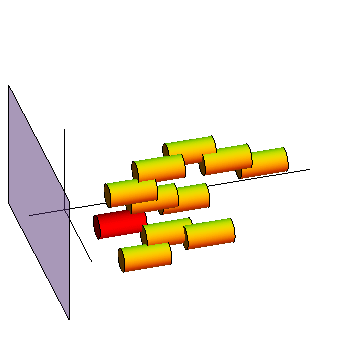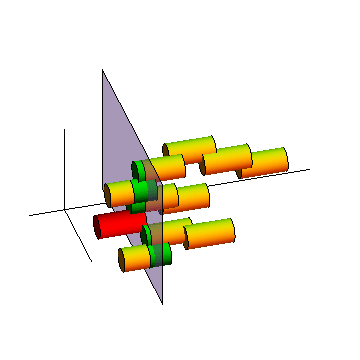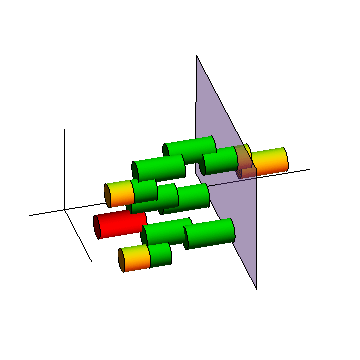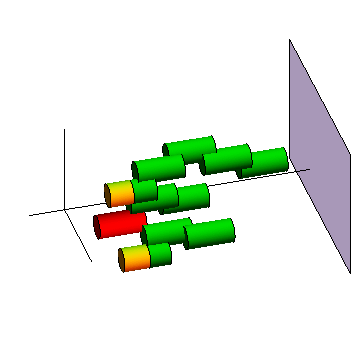
Figure: Message dissemination in space-time with stationary nodes.
Table: Critical thresholds.
| System | νc |
|---|
| Disks in plane: | 4.51 |
| Aligned cylinders, directed: | 1.52 |
| Aligned cylinders, undirected: | 1.32 |
|

